La gravedad, considerada una de las cuatro interaccionen fundamentales del Universo, es la que nos mantiene pegados al suelo y hace que caigan los objetos. Así mismo, es la responsable de los movimientos de todos los objetos en el Universo, como que la Luna se mueva alrededor de la Tierra, que los planetas orbiten alrededor del Sol o que los miles de millones de estrellas que forman una galaxia giren alrededor del centro de ésta como si fuera un gigantesco remolino.
El concepto de gravedad puede explicarse desde dos perspectivas diferentes: desde la mecánica clásica de Isaac Newton o mediante las revolucionarias ideas de Albert Einstein.
Ambas interpretaciones de la gravedad supusieron, cada una en su época, un gran paso adelante en el conocimiento científico; ambas siguen siendo válidas y ampliamente utilizadas por la ciencia para explicar diferentes fenómenos físicos en el Universo.
La Gravedad según Isaac Newton.
Issac Newton (1643-1727) publicó en 1687 lo que muchos científicos creen que es el libro más importante de la historia de la ciencia: Philosophiae Naturalis Principia Mathematica, donde establece por primera vez una relación proporcional de la fuerza con que se atraen dos objetos con masa, dando a entender los fenómenos físicos más importantes del universo observable y explicando las tres leyes de Kepler.
Esta relación proporcional es la que constituye la denominada Ley de Gravitación Universal que, más de trescientos años después, sigue en vigor.
Lo que dice esta ley es que dos cuerpos con masa experimentan una fuerza de atracción entre ellos que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.
Pues ya sabemos que la Tierra y la Luna se atraen con una fuerza que se puede calcular con esta fórmula; al igual que la Tierra y el Sol, Júpiter y sus satélites, y cualquier cuerpo con masa en el Universo.
A la vista de esta fórmula podemos darnos cuenta de que esta fuerza es muy muy débil porque la constante gravitacional G es extremadamente pequeña: cero coma, cero, cero, cero,.....(hasta diez ceros), 6674. Por eso podemos pensar que dos canicas, por ejemplo, en el espacio no van a experimentar mucha fuerza de atracción entre ellas debido a sus pequeñas masas; aunque en ausencia de otras fuerzas y con el tiempo llegarían a unirse. Pero cuando se trata de objetos con mucha masa, como estrellas o planetas, las fuerzas gravitatorias ya son considerables. Y ya no hablemos de objetos supermasivos como estrellas gigantes, estrellas de neutrones o incluso agujeros negros.
Bien, pero ahora podríamos preguntarnos: por qué, dada la fuerza con la que se atraen, la Tierra y la Luna no se precipitan una contra la otra y acaban colisionando?
Imaginemos el caso mostrado en la siguiente figura:
Un arquero situado en cualquier lugar de la Tierra dispara una flecha en dirección horizontal, paralela al suelo, con una velocidad V1 (situación 1). Nada más disparar la flecha, ésta es frenada por el rozamiento con el aire a la vez que es atraída hacia el suelo por la gravedad terrestre, recorriendo una distancia determinada hasta que cae al suelo.
Supongamos que no hay atmósfera (situación 2). La flecha, lanzada a la misma velocidad V1 no sufre el frenado debido a la resistencia del aire pero sí el efecto de la gravedad terrestre; por tanto, también termina cayendo al suelo pero ha recorrido una distancia mayor.
Ahora supongamos que la flecha es lanzada a una velocidad V2>V1 (situación 3) tal que, al tiempo que va cayendo al suelo, se encuentra que, debido a la curvatura de la superficie terrestre, nunca llega a alcanzar el suelo. La flecha ha entrado en órbita alrededor de la Tierra.
Es decir, que podemos afirmar que la Luna está permanentemente cayendo hacia la Tierra pero nunca llega a caer al suelo. Y lo mismo le ocurre a la Tierra orbitando alrededor del Sol o a cualquier astro que está orbitando alrededor de otro.
Otra pregunta que podríamos hacernos es: cual es la velocidad a la que debe orbitar la Luna para mantenerse siempre a esa distancia de la Tierra y no caer hacia ella?
Resulta fácil de calcular: por un lado, mediante la fórmula de la gravitación universal de Newton, conociendo la masa de la Tierra m1, la masa de la Luna m2 y la distacia que las separa r, sabremos el valor de la fuerza de atracción gravitatoria Fg.
Por otro lado sabemos que cuando un cuerpo recorre una trayectoria curva sufre una fuerza centrífuga Fc que le impulsa hacia el exterior de la curva (como cuando tomamos una curva en el coche y nos sentimos empujados hacia fuera). Para que la Luna se mantenga a la distancia adecuada de la Tierra, la fuerza centrífuga Fc debe ser igual a la fuerza de atracción gravitatoria Fg, y como la fuerza centrífuga depende de la velocidad, podemos calcular ésta (tampoco vamos a discutir aquí cómo se calcula la velocidad a partir de la fuerza centrífuga).
La Ley de la Gravitación Universal de Newton ofrece una interprtación de la gravedad bastante exacta y, de hecho, es la base principal de todos los cálculos que los físicos realizan para calcular las órbitas de los astros, para enviar naves a la Luna, sondas a Marte o, incluso, para poner satélites artificiales en órbita alrededor de la Tierra.
La Gravedad según Albert Einstein.
Albert Einstein (1879-1955) publicó, a principios del siglo XX, su mundialmente conocida como Teoría de la Relatividad, que consta de dos partes: la Teoría de la Relatividad Especial, publicada en 1905 y que trata de la física del movimiento de los cuerpos en ausencia de fuerzas gravitatorias, y la Teoría de la Relatividad General, publicada en 1915 y que trata de la interacción gravitatoria.
Es esta segunda parte la que nos interesa analizar en este artículo.
El 29 de mayo de 1919 tuvo lugar un eclipse total de Sol que los científicos de la época aprovecharon para comprobar una de las afirmaciones de la Teoría de la Relatividad General que Albert Einstein había publicado sólo cuatro años antes: la trayectoria de un rayo de luz se curva al atravesar un campo gravitatorio.
En efecto, lo que se observó durante aquel eclipse es que una determinada estrella, cuya posición real en el cielo era perfectamente conocida, aparecía desviada de su posición en un ángulo predicho con total exactitud por la Teoría de la Relatividad General.
Parece que el rayo de luz procedente de la estrella se ha desviado hacia el Sol como si la gravedad producida por éste lo hubiera atraído.
La Ley de Gravitación Universal de Newton dice que la fuerza de atracción gravitatoria se produce entre cuerpos con masa, pero .... la luz no tiene masa !!!. Qué ocurre entonces??
Pues que nos encontramos con la idea más revolucionaria de la historia de la ciencia: un cuerpo con masa deforma el espacio a su alrededor; es decir, la gravedad es la curvatura del espacio producida por un cuerpo con masa.
Pero cómo se va a curvar el espacio?. Podríamos interpretarlo como una curvatura en una cuarta dimensión física que, evidentemente, no podemos apreciar porque nosotros estamos "atrapados" en tres dimensiones físicas.
Para facilitar esta visualización imaginemos que el espacio tiene sólo dos dimensiones y que la presencia de un objeto con masa produce una curvatura en una tercera dimensión que, los habitantes de ese universo bidimensional no pueden ver.
El rayo de luz procedente de la estrella no ha variado su trayectoria, es el propio espacio el que se ha curvado obligando al rayo de luz a desplazarse por ese espacio curvo.
Lo mismo ocurre cuando un astro está en órbita alrededor de otro más masivo. Por ejemplo, la Luna orbita alrededor de la Tierra no obligada por una fuerza gravitatoria sino obligada a moverse por un espacio curvo en perpetua caída hacia la Tierra sin alcanzarla jamás.
Algo parecido a lo que podemos ver en la siguiente imagen:
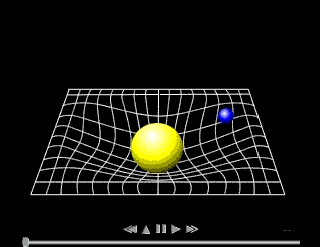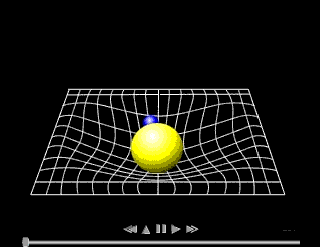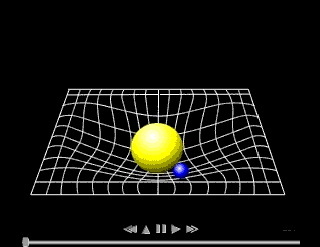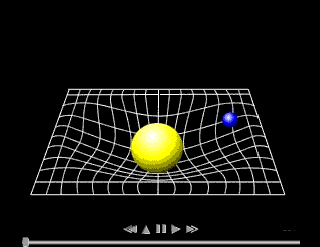
Un astuto profesor de la Facultad de Física de la Universidad Pontificia de Chile quiso explicar ésto a sus alumnos y tuvo la idea de utilizar una tela elástica para simular el espacio y unas bolas de metal que representaban los cuerpos con masa y realizó los siguientes experimentos:
En este vídeo muestra cómo un objeto con masa deforma el espacio de modo que un segundo objeto es atraído por él y acaban colisionando sin que haya intervenido ninguna fuerza.
En este otro vídeo ha querido mostrar cómo la curvatura del espacio producida por el campo gravitatorio del Sol "atrapa" los planetas del Sistema Solar, cada uno en su órbita.
Evidentemente el experimento es bastante rudimentario porque las bolas de metal se ven frenadas por el rozamiento con la tela elástica y rápidamente caen hacia el centro; pero en el espacio no hay ningún rozamiento que frene a los planetas y, por tanto, están girando alrededor del Sol indefinidamente.
Podría decirse que la Teoría de la Relatividad es la idea científica más revolucionaria de la historia de la ciencia. Lo que hemos visto en este artículo es solamente una breve "pincelada" de la teoría, puesto que su contenido es muchísimo más extenso y ofrece planteamientos muy novedosos sobre muchos otros conceptos de la física. Quizás la idea más "perturbadora" de la teoría es que afirma que no existe separación entre espacio y tiempo. De hecho, cada vez que he utilizado la palabra "espacio" en esta sección del artículo, debería haber dicho "espacio-tiempo". Y es que la gravedad no solamente distorsiona el espacio, también el tiempo. Espacio y tiempo son inseparables. Pero ésto ya sería tema para otro artículo más extenso.
El concepto de gravedad puede explicarse desde dos perspectivas diferentes: desde la mecánica clásica de Isaac Newton o mediante las revolucionarias ideas de Albert Einstein.
Ambas interpretaciones de la gravedad supusieron, cada una en su época, un gran paso adelante en el conocimiento científico; ambas siguen siendo válidas y ampliamente utilizadas por la ciencia para explicar diferentes fenómenos físicos en el Universo.
La Gravedad según Isaac Newton.
Esta relación proporcional es la que constituye la denominada Ley de Gravitación Universal que, más de trescientos años después, sigue en vigor.
Lo que dice esta ley es que dos cuerpos con masa experimentan una fuerza de atracción entre ellos que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.
|
|
G es una constante física universal cuyo valor y unidades no vamos a discutir aquí por quedar fuera del objetivo de este artículo |
Pues ya sabemos que la Tierra y la Luna se atraen con una fuerza que se puede calcular con esta fórmula; al igual que la Tierra y el Sol, Júpiter y sus satélites, y cualquier cuerpo con masa en el Universo.
A la vista de esta fórmula podemos darnos cuenta de que esta fuerza es muy muy débil porque la constante gravitacional G es extremadamente pequeña: cero coma, cero, cero, cero,.....(hasta diez ceros), 6674. Por eso podemos pensar que dos canicas, por ejemplo, en el espacio no van a experimentar mucha fuerza de atracción entre ellas debido a sus pequeñas masas; aunque en ausencia de otras fuerzas y con el tiempo llegarían a unirse. Pero cuando se trata de objetos con mucha masa, como estrellas o planetas, las fuerzas gravitatorias ya son considerables. Y ya no hablemos de objetos supermasivos como estrellas gigantes, estrellas de neutrones o incluso agujeros negros.
Bien, pero ahora podríamos preguntarnos: por qué, dada la fuerza con la que se atraen, la Tierra y la Luna no se precipitan una contra la otra y acaban colisionando?
Imaginemos el caso mostrado en la siguiente figura:
Un arquero situado en cualquier lugar de la Tierra dispara una flecha en dirección horizontal, paralela al suelo, con una velocidad V1 (situación 1). Nada más disparar la flecha, ésta es frenada por el rozamiento con el aire a la vez que es atraída hacia el suelo por la gravedad terrestre, recorriendo una distancia determinada hasta que cae al suelo.
Supongamos que no hay atmósfera (situación 2). La flecha, lanzada a la misma velocidad V1 no sufre el frenado debido a la resistencia del aire pero sí el efecto de la gravedad terrestre; por tanto, también termina cayendo al suelo pero ha recorrido una distancia mayor.
Ahora supongamos que la flecha es lanzada a una velocidad V2>V1 (situación 3) tal que, al tiempo que va cayendo al suelo, se encuentra que, debido a la curvatura de la superficie terrestre, nunca llega a alcanzar el suelo. La flecha ha entrado en órbita alrededor de la Tierra.
Es decir, que podemos afirmar que la Luna está permanentemente cayendo hacia la Tierra pero nunca llega a caer al suelo. Y lo mismo le ocurre a la Tierra orbitando alrededor del Sol o a cualquier astro que está orbitando alrededor de otro.
Otra pregunta que podríamos hacernos es: cual es la velocidad a la que debe orbitar la Luna para mantenerse siempre a esa distancia de la Tierra y no caer hacia ella?
Resulta fácil de calcular: por un lado, mediante la fórmula de la gravitación universal de Newton, conociendo la masa de la Tierra m1, la masa de la Luna m2 y la distacia que las separa r, sabremos el valor de la fuerza de atracción gravitatoria Fg.
Por otro lado sabemos que cuando un cuerpo recorre una trayectoria curva sufre una fuerza centrífuga Fc que le impulsa hacia el exterior de la curva (como cuando tomamos una curva en el coche y nos sentimos empujados hacia fuera). Para que la Luna se mantenga a la distancia adecuada de la Tierra, la fuerza centrífuga Fc debe ser igual a la fuerza de atracción gravitatoria Fg, y como la fuerza centrífuga depende de la velocidad, podemos calcular ésta (tampoco vamos a discutir aquí cómo se calcula la velocidad a partir de la fuerza centrífuga).
La Ley de la Gravitación Universal de Newton ofrece una interprtación de la gravedad bastante exacta y, de hecho, es la base principal de todos los cálculos que los físicos realizan para calcular las órbitas de los astros, para enviar naves a la Luna, sondas a Marte o, incluso, para poner satélites artificiales en órbita alrededor de la Tierra.
La Gravedad según Albert Einstein.
Es esta segunda parte la que nos interesa analizar en este artículo.
El 29 de mayo de 1919 tuvo lugar un eclipse total de Sol que los científicos de la época aprovecharon para comprobar una de las afirmaciones de la Teoría de la Relatividad General que Albert Einstein había publicado sólo cuatro años antes: la trayectoria de un rayo de luz se curva al atravesar un campo gravitatorio.
En efecto, lo que se observó durante aquel eclipse es que una determinada estrella, cuya posición real en el cielo era perfectamente conocida, aparecía desviada de su posición en un ángulo predicho con total exactitud por la Teoría de la Relatividad General.
Parece que el rayo de luz procedente de la estrella se ha desviado hacia el Sol como si la gravedad producida por éste lo hubiera atraído.
La Ley de Gravitación Universal de Newton dice que la fuerza de atracción gravitatoria se produce entre cuerpos con masa, pero .... la luz no tiene masa !!!. Qué ocurre entonces??
Pues que nos encontramos con la idea más revolucionaria de la historia de la ciencia: un cuerpo con masa deforma el espacio a su alrededor; es decir, la gravedad es la curvatura del espacio producida por un cuerpo con masa.
Pero cómo se va a curvar el espacio?. Podríamos interpretarlo como una curvatura en una cuarta dimensión física que, evidentemente, no podemos apreciar porque nosotros estamos "atrapados" en tres dimensiones físicas.
Para facilitar esta visualización imaginemos que el espacio tiene sólo dos dimensiones y que la presencia de un objeto con masa produce una curvatura en una tercera dimensión que, los habitantes de ese universo bidimensional no pueden ver.
El rayo de luz procedente de la estrella no ha variado su trayectoria, es el propio espacio el que se ha curvado obligando al rayo de luz a desplazarse por ese espacio curvo.
Lo mismo ocurre cuando un astro está en órbita alrededor de otro más masivo. Por ejemplo, la Luna orbita alrededor de la Tierra no obligada por una fuerza gravitatoria sino obligada a moverse por un espacio curvo en perpetua caída hacia la Tierra sin alcanzarla jamás.
Algo parecido a lo que podemos ver en la siguiente imagen:
Un astuto profesor de la Facultad de Física de la Universidad Pontificia de Chile quiso explicar ésto a sus alumnos y tuvo la idea de utilizar una tela elástica para simular el espacio y unas bolas de metal que representaban los cuerpos con masa y realizó los siguientes experimentos:
En este vídeo muestra cómo un objeto con masa deforma el espacio de modo que un segundo objeto es atraído por él y acaban colisionando sin que haya intervenido ninguna fuerza.
En este otro vídeo ha querido mostrar cómo la curvatura del espacio producida por el campo gravitatorio del Sol "atrapa" los planetas del Sistema Solar, cada uno en su órbita.
Evidentemente el experimento es bastante rudimentario porque las bolas de metal se ven frenadas por el rozamiento con la tela elástica y rápidamente caen hacia el centro; pero en el espacio no hay ningún rozamiento que frene a los planetas y, por tanto, están girando alrededor del Sol indefinidamente.
Podría decirse que la Teoría de la Relatividad es la idea científica más revolucionaria de la historia de la ciencia. Lo que hemos visto en este artículo es solamente una breve "pincelada" de la teoría, puesto que su contenido es muchísimo más extenso y ofrece planteamientos muy novedosos sobre muchos otros conceptos de la física. Quizás la idea más "perturbadora" de la teoría es que afirma que no existe separación entre espacio y tiempo. De hecho, cada vez que he utilizado la palabra "espacio" en esta sección del artículo, debería haber dicho "espacio-tiempo". Y es que la gravedad no solamente distorsiona el espacio, también el tiempo. Espacio y tiempo son inseparables. Pero ésto ya sería tema para otro artículo más extenso.
Qué interesante! Siempre me ha gustado la teoría de la relatividad pero necesito más conceptos físicos. Y lo de que no exista separación entre espacio y tiempo es lo máximo!
ResponderEliminar